Instability
Instability is not always easy to recognize. In this section we try to describe the most common cases and, of course, how to solve or avoid the problems related to that computational instability.
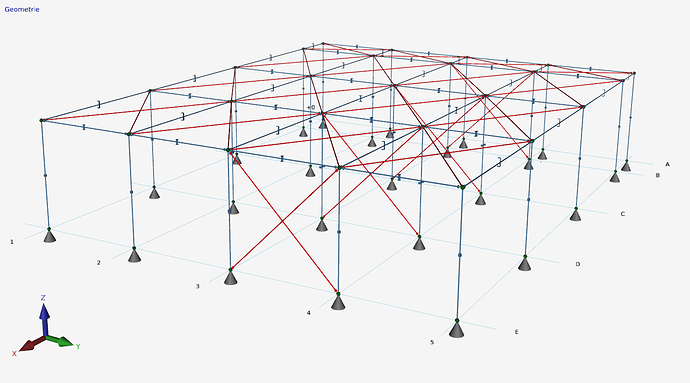
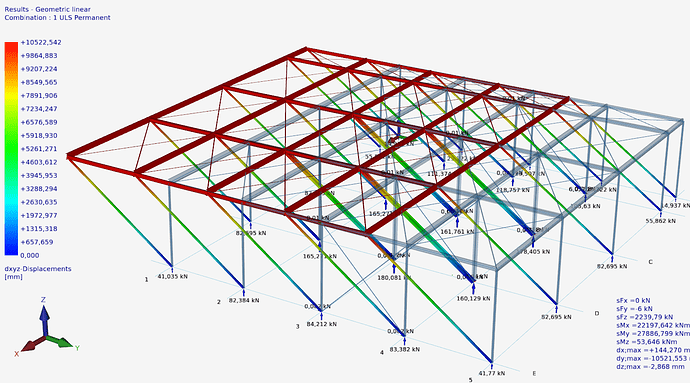
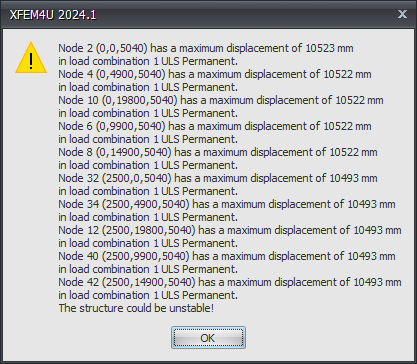
The model below is unstable and combination 1.ULS Permanently shows large displacements (10523 mm) in y-direction. While calculating, XFEM4U also gives you a warning
This is a classical example though. Almost all beams are purely hinged connected and the bracings (hinged tensile beams in red) should make the structure stable.
trekstaven.xfem (130.7 KB)
What is going on here?
In the calculation of the force distribution in the combinations, tension beams “disappear” automatically (in the iterative GL and GNL calculation process, respectively) when compressive forces occur in them or when the tension beams shorten. In the first combination (1. ULS Permanent) apparently all tension beams (all bracings) disappear simultaneously and what is left is a “card house”. Mathematically this means: The global stiffness matrix becomes singular, or approaches singularity and therefore cannot be solved. (The determinant of the matrix becomes zero or approaches zero.)
Ok - but how to solve it?
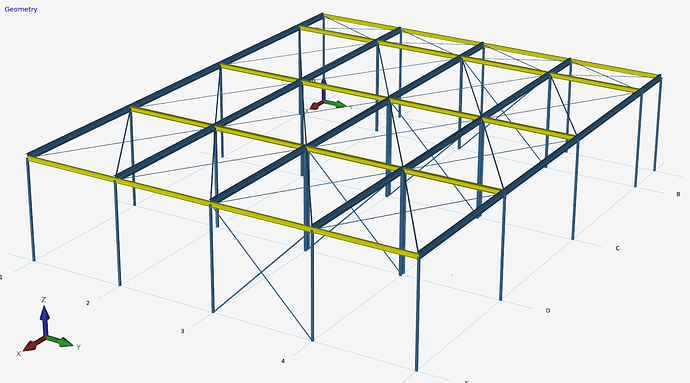
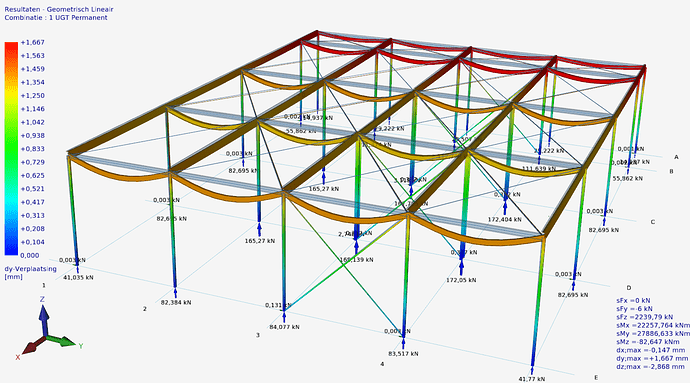
Make the beam connections (joints) moment fixed but with a small spring value. And that is what I have done here. See below and the appendix.
It’s a better schematization anyway. Purely hinged connections virtually do not exist in steel structures like here. There is always some spring-loaded trapping. The Ry spring value chosen here is so small that it causes hardly any bending moments but ensures that the model remains computationally stable in all cases.
trekstaven1.xfem (130.7 KB)
Kind regards
Rob Baaij